Cryptography
Cryptography is a method for changing or making unreadable the data for security reasons when transmitting or storing. Cryptography is an indispensable requirement for today's communication systems. There are several methods for encryption but cryptosystems can be grouped under the two main titles.
- Symmetric cryptosystems
- Asymmetric cryptosystems
Symmetric encryption systems use the same key to encrypt and decrypt data, while asymmetric systems use different keys. AES, Serpent, Twofish and Kuznyechick are the some of examples of symmetric cryptosystems, while some asymmetric cryptosystems are RSA and Elliptic Curve.
Rijndael
Rijndael (known as AES) is a symmetric cryptosytem. Since it is symmetric, AES uses the same key for encryption and decryption and in most cases AES is a preferable secure and high performance solution due to the simplicity of mathematical operations.
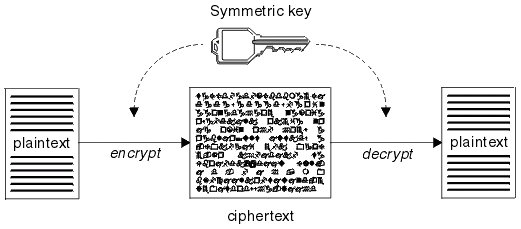
Source: https://rsec.kr/
You can find a comic style full explanation of AES encryption and decryption scheme from here.
Rivest Shamir Adleman
Rivest-Shamir-Adleman (RSA) is a widely used public-key cryptosystem. It's based on semi-prime numbers which are multiplication of two prime numbers. The prime numbers can be divided by only one and itself. Without prior knowledge about keys, revealing the numbers is a difficult factoring problem because of a typical RSA cryptosystem uses quite large numbers for keys.

A simple RSA algorithm uses two different prime numbers \(p\) and \(q\). The multiplication of these two numbers gives us a semi-prime number which is called modulus \(n\). Modulus determines the length of the cryptosystem. Using the additional two numbers which one is public exponent \(e\) and the other is private exponent \(d\) the cryptosystem is defined.
\begin{equation} Public\ key = (e,n) \\ Private\ key = (d,n) \end{equation}While encryption is achieved by using public exponent and modulus, for the decryption the user only needs to private exponent and modulus.
\begin{equation} c = (m)^e \ mod\ n \end{equation} \begin{equation} m = (c)^d \ mod\ n \end{equation}Elliptic Curve Cryptography
Elliptic curve cryptography is a new approach to the public-key cryptosystems. Since RSA is getting weaker and weaker with increasing processing capabilities of the computers, elliptic curve will be more preferred cryptosystem. Elliptic curve cryptography is a based on a shape like below.

Source: https://www.allaboutcircuits.com/
The plaintext message is converted to a point at the plane using the formula of this shape. For example, X coordinate of this point can be chosen equal to message and Y coordinate can be evaluated.
\begin{equation} y^2=x^3+Ax+B\ (mod\ p) \end{equation}Let's assume the point holds the message is represented with \(M\), the ciphertext is formed by using \(C_1\) and \(C_2\) where \(r\) is a random number, \(G\) is the base point of the curve and \(K\) is the public key.
\begin{equation} C_1 = M + rK \\ C_2 = r\ G \end{equation}For decryption only \(C_1\) and \(C_2\) send to receiver and with private key \(k\) and using the equation below the message can be recovered.
\begin{equation} M=C_1-k\ C_2 \end{equation}