
A Library to Create Kaleidoscope Effect
Kaleidoscope is derived from Ancient Greek and it means observation of beautiful forms according to Wikipedia [1]. But what is this effect and how this effect is generated? First of all take a look at the logo above. Did you see the hexagons replacing the "o" characters? This is the simplest example of kaleidoscope effect for a triangle. Simply you are rotating and concataneting the triangles to form a hexagon shape. So this is a kaleidoscope image of a triangle with six rotations. See the image below.
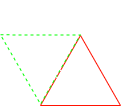

Rotation of cropped image to generate effect
But how is this possible for images with rectangular or even with different types of images? Just by cropping and scaling them. For example assume we have 1920x1080 resolution image. This means that we have a rectangular image. So for the generating effect with n image rotation we have to determine the triangle. By using two sides and an angle between them we can calculate all of the properties of this angle. Also for the effect the triangle is isosceles. So, since for the effect generation n image rotation is requested,
\begin{equation} {\alpha}=360/n \end{equation} \begin{equation} h_{triangle}=min(\frac{w_{image}}{2\;tan(\alpha / 2)}, h_{image}) \end{equation} \begin{equation} \frac{w_{triangle}}{2}=h_{triangle}\;tan(\alpha / 2) \end{equation}All of the required properties of triangle is defined so what's next? Scaling and rotating them! For the library, I used a transformation map to hold these information since the source and destination pixels will be constant for the same resolution and number of rotations. So while the initialization function consumes more memory and processing time, on fly operations will be faster. Where \(\varphi\) is the rotation angle, the source and destination pixel coordinates are defined as,
\begin{equation} x_{dest}=x\;cos(\varphi) + y\;sin(\varphi) \end{equation} \begin{equation} y_{dest}=y\;cos(\varphi) + x\;sin(\varphi) \end{equation}Now we know the which pixels are involved in the effect and we have source and destination pixel maps. So we can apply the transformation! Just take the source image and copy pixels to destination image according to map. That's it! See an example image below for the kaleidoscope effect.
 (a)
(a)
 (b)
(b)
An example to applied effect with number of rotations is six.
You can find the library in GitHub from here or the developer documentation here.
- [1] Wikipedia Kaleidoscope Entry https://en.wikipedia.org/wiki/Kaleidoscope