Source Localization
Signals have different propagation speeds depending on their nature and environmental characteristics. As a result of propagation, every sensor (if their positions are different) will record delayed signals. Direction of arrival of the signal can be estimated by using these delays.
The delay between two signals can be determined using the cross-correlation. The cross-correlation between two signals \(S_1\) and \(S_2\) described as (1). Maximum amplitude value of cross-correlation gives us the lag \((\Delta t)\) between two input signals.
\begin{equation} R_{S_1 S_2} = \mathrm{E}[S_1 S_2^*] = \int \int S_1 S_2 f_{S_1 S_2}(S_1,S_2) dS_1 dS_2 \end{equation}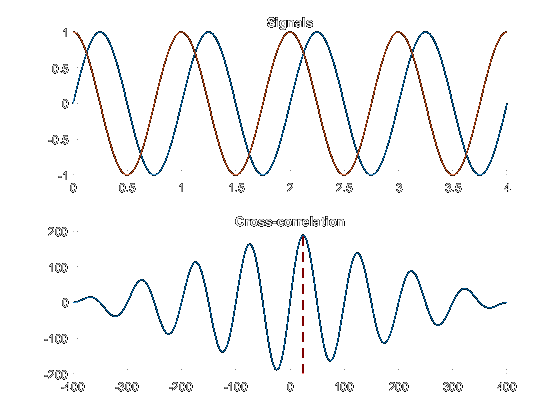
Cross-correaltion between two sinusoids.
As mentioned the time difference is related with propagation speed \((V)\) and distance so, if the propagation speed and time difference are known with (2) the difference of distance along the wave path \((\Delta x)\) can be found.
\begin{equation} \Delta x=V\times \Delta t \end{equation}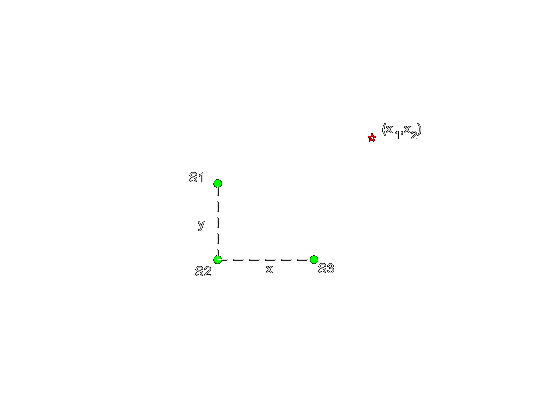
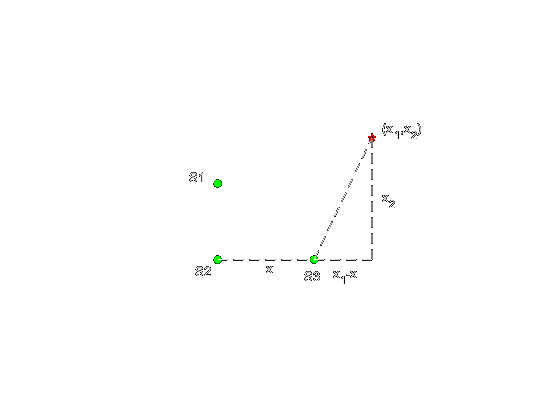
If we have limited number of sensors it is possible to couple them to estimate \(\Delta x\) distances and locate source. But if we have \(n\) sensors, calculation process will be more complex. To ease the process and obtain more generalized solution, distance from \(n\) sensors to source can be determined with \(n\) different equation. Assume we have identical three sensors and one signal source at \((x_s,y_s)\) distances from sensor can be defined by using three nonlinear equations.
\begin{equation} \begin{split} x_s^2+(y_s-y_1)^2=(r+a)^2 \\ x_s^2+y_s^2=(r+b)^2 \\ (x_s-x_3)^2+y_s^2=(r+c)^2 \end{split} \end{equation}This equation set can be solved by using Newton-Raphson method. With this method, coordinates of source \((x_s,y_s)\) estimated iteratively using Jacobian matrix (3).
\begin{equation} J= \left[ {\begin{array}{ccc} 2x_s & 2y_s-2y_1 & -2r-2a \\ 2x_s & 2y_s & -2r-2b \\ 2x_s-2x_3 & 2y_s & -2r-2c \end{array}} \right] \end{equation}MATLAB implementation of this method can be downloaded from here (Non-commercial use only). This application reads data from analog to digital converters (ADC) belongs to National Instruments in real time and every time step estimates the source location.

Screenshot of initiliazer of MATLAB application.
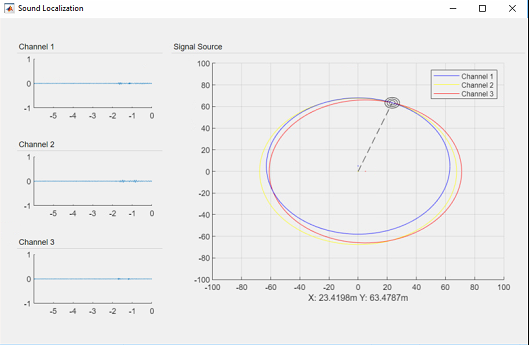
Real-time source localization of application.